奥妙的毕氏定理|星岛教室
2024-12-19 11:40 
我们学习数学一定学习过直角三角形,当中有一个著名的理论——毕氏定理(Pythagorean theorem)。生活中我们不知不觉地应用这个理论。其实毕氏定理不仅是数学中的基础理论,还在现代生活和技术中有许多实际应用,例如过马路、走斜坡、走捷径等,都经常运用毕氏定理。
何谓「毕氏定理」?
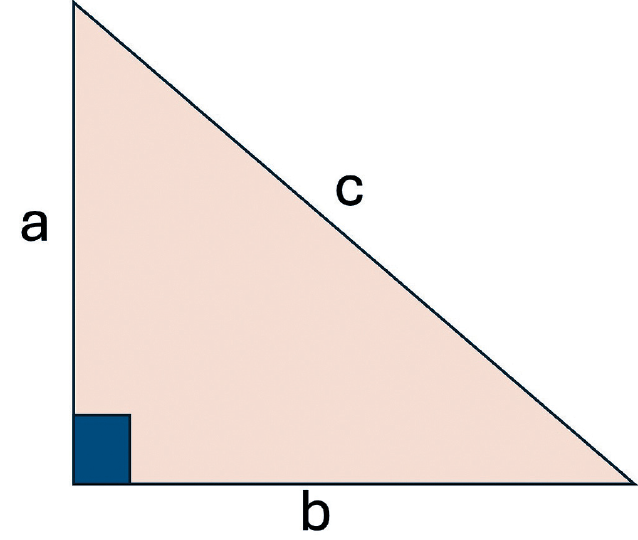
这个定理告诉我们,直角三角形中的两条短边的平方和等于长边的平方。这条长边叫做斜边,也是直角对面的那条边。
「毕氏定理」的公式是: a2+b2=c2
a和b是直角三角形的两条边
c是斜边(最长的那条边)
假设一个直角三角形,它的两条边长(a和b)分别是3米和4米。你可以用毕氏定理来计算斜边的长度:32+42=c2,即是,9+16=c2,所以:25=c2,√25=c,5=c。因此,我们可用此方法找出斜边的长度是5米。
生活解难
1. 最短路线

在一条繁忙的街道上,想由红点走到红色箭嘴。你可以先沿着橙色路线,连续过两条斑马线,亦可以直接沿着蓝色路线走,这样更快,更省时间。你可以用毕氏定理来计算这条最短的蓝色路线的距离。
假设其中一条路线长40米,另一路线长30米,你想知道由红点走到红色箭嘴的最短距离,我们可以根据毕氏定理,计算蓝色路线的长度:302+402=蓝色路线2,√2500=蓝色路线,蓝色路线的长度是50米。换言之,如果我们走蓝色路线的路程,比过两条斑马线(30+40=70)短。
2. 滑梯长度
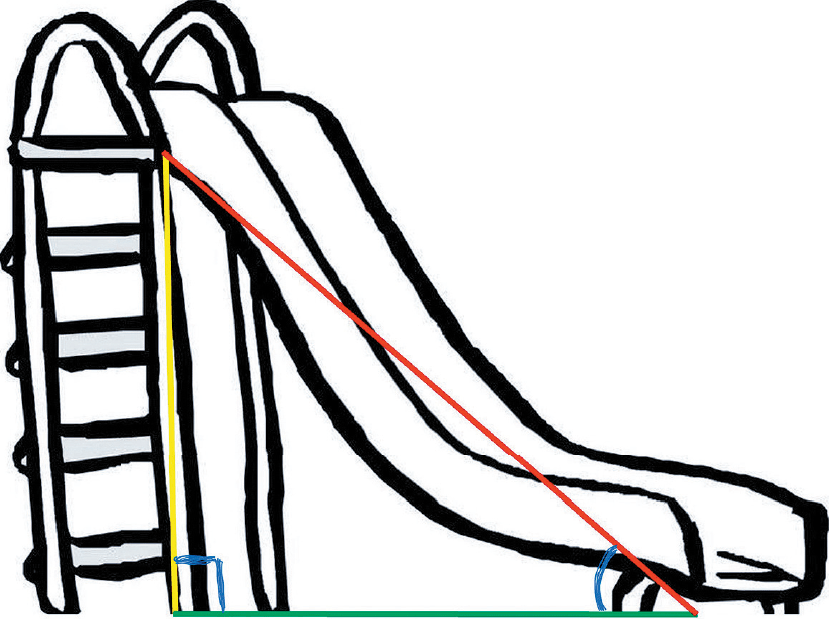
滑梯是我们经常玩的玩具,设计者常须计算滑梯的实际长度,以确保滑行的舒适性和安全性。这个长度可通过毕氏定理来计算,当我们已知滑梯的高度和水平距离时,滑梯长度就是这两者形成的直角三角形的斜边。
图3是一个滑梯,黄色线是1米高,绿色线有1.5米长,黄色线和绿色线是互相垂直,因此可通过毕氏定理来计算红色线滑梯的长度:12+1.52=滑梯长度2,即是√3.25=滑梯的长度,那么滑梯的长度约1.8米。
另外,滑梯的长度和坡度会直接影响滑行的速度和感受。通过计算滑梯的实际长度,设计师便可确保滑梯的坡度不会过于陡峭,从而提供一个既安全又有趣的滑行体验。假若坡度较平缓的滑梯,适合儿童使用,这样,黄色线高度保持不变,而绿色水平线延长至3米,如此绿色水平线与红色斜边的角度会降低,而红色线的长度可利用毕氏定理来计算:平缓滑梯长度=√(12+32)=√103.16米。换言之,如要坡度较低,较平缓的滑梯,需要水平长度和斜边长度较长的滑梯。
3. 最短路径
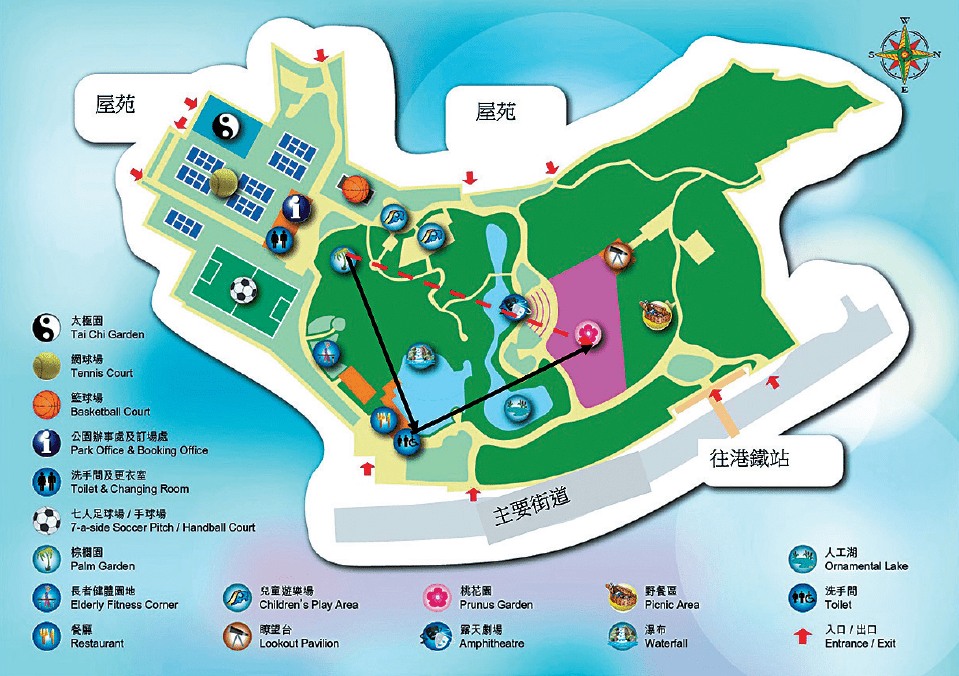
我们要走出一个面积大的地方,捷径是最快又最省力的方法。如果你在公园的棕榈园,想走到桃花园。你可以有两个选择︰先沿着黑色路线,经过餐厅和厕所,然后再经过第二条黑色路线,再到桃花园,这个方法不但浪费时间,又浪费力气;但走红色路线会更快。这个时候,你可以用毕氏定理来计算这条最短的红色线路程。
假设公园的一边是30米,另一边是40米,你想知道走对角线的最短距离是多少。根据毕氏定理,我们可以计算出从棕榈园到桃花园最近的距离:302+402=棕榈园到桃花园最近的距离2,即是√2500=棕榈园到桃花园最近的距离,因此从棕榈园到桃花园最近的距离是50米。换言之,在一个直角三角形里,构成直角的两条边长长度相加一定是比斜边长,所以斜边是最短的。
GPS计算距离
GPS(全球定位系统)的运作原理中涉及大量数学计算,其中包括毕氏定理的应用。虽然GPS本身运用了更为复杂的数学(如三角测量和相对论效应),但在某些情况下,毕氏定理可用来解决GPS定位中的问题,特别是当我们处理平面距离或简单的距离计算时。
毕氏定理在全球定位系统(GPS)中非常重要。GPS通常依赖于从多颗卫星发送的信号来确定某个物体或人的位置。每颗卫星会发送到达接收器的信号,GPS接收器可根据这些信号计算出两个地方之间的距离。
当然,我们只考虑在地球上水平平面上的定位,就可以使用毕氏定理来进行简化计算。当我们知道某个点的经纬度时,通过毕氏定理就可以计算两点之间的直线距离。
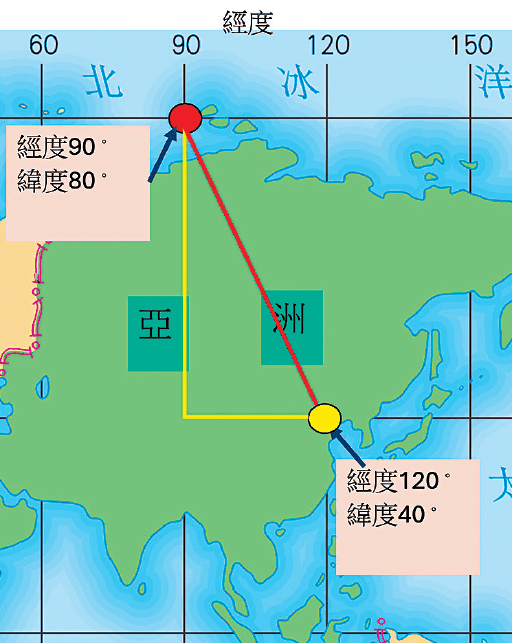
例如:假设GPS确定了两个点的水平位置,该点是红点(经度90度,纬度80度)与黄点(经度120度,纬度40度),即是垂直黄色线是纬度相减(80度-40度)=40单位,而水平黄色线是经度相减(120度-90度)=30单位。此时,我们可用毕氏定理来计算两点之间的直线距离,即平面上最短距离。
根据毕氏定理:
两点距离=√(402+302)=√2500=50单位
因此,红点与黄点之间的直线距离为50单位。这种情况下,GPS接收器可知道自己在平面上的具体位置,并根据位置与其他点距离进行计算。
毕氏定理不仅仅是一个数学公式,它在日常生活中有许多应用。无论是计算斜台的长度、走最短的路,还是GPS上的应用,毕氏定理是一个非常有用的工具来计算平面或空间中的直线距离。无论是在导航、计算水平距离,还是高度差的问题中,毕氏定理都能提供简单而有效解法。希望你能通过这些例子,学会在生活中应用毕氏定理。
小思考,大智慧
如果遇到非直角三角形的生活难题,我们可以应用哪些理论?
参考答案
我们可使用其他数学工具来解决,比如「正弦定理」和「馀弦定理」。这些定理都可以帮助我们处理非直角三角形中的边长和角度计算,并且在很多实际应用中皆非常有用。
本栏逢周四刊登,由教育评议会邀请资深中小学老师、校长及大学讲师撰稿,旨在为学生提供多元化的STEAM学习材料,引发学生探求知识的兴趣,将学习融入生活,培养学生的世界观、敏锐的触觉、积极学习的态度。
文:中华基督教会蒙黄花沃纪念小学数学科主任 叶剑㷨、中华基督教会蒙黄花沃纪念小学老师周伟强博士
延伸阅读:











最新回应